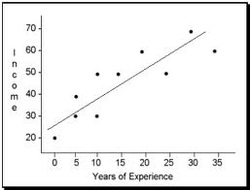
Now, imagine that we got a correlation of 0.4 after testing the sample of 30 people. How do we know that such correlation occurs in the population as well? And, how do we know if the size of our sample was sufficiently big to be representative?
In this post, I will explain what is meant by significance testing. In practice, it does not involve any calculation; in fact, there is a ready-made table of significance which simply tells you whether your result is significant enough or not depending on your sample size and correlation coefficient. However, I think it is important to understand the logic behind this table - and this is exactly what I will attempt to explain in this post. I will give the table in the end as well, so if you are not really interested in theoretical considerations at the moment you can safely go straight there.