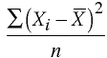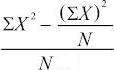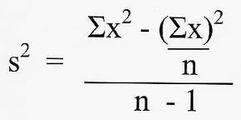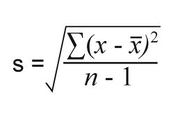There are also two great video lessons made by Khan Academy, which explain variance in a very easy to follow and entertaining way.
Variability
Consider two following score sets: 2, 2, 2, 2, 2 and 8, 1, 2, 1, 1, 1, 1, 1. Ok, the examples are not great but they do illustrate the point: the mean equals 2 in each set, however it is obvious that variability is larger in the second set. It means that the score 2 is less representative for that set than for the first one, and we need to take it into account.
So, to make sure we account for variability, we need to find the deviation from the mean for each score in our set; in other words, to calculate how much bigger or smaller it is than the mean. To do so, simply subtract the mean from each of the scores. For example, for the second set that we have:
SCORE - MEAN Deviation from mean
8 - 2 6
1 - 2 -1
2 - 2 0
1 - 2 -1
1 - 2 -1
1 - 2 -1
1 - 2 -1
1 - 2 -1
We can then calculate the mean deviation - in exactly the same way you would calculate the mean for your scores. But an interesting thing happens: it will always leave you with zero due to the negative values of some of the deviations. So how do we find a single figure which would tell us how variable our data is?
This is where variance makes an entrance, making statisticians' lives much easier by getting rid of all those negatives. There are two simple steps to finding it:
1. Square each deviation. It leaves us with following:
SCORE - MEAN Deviation from the mean Square
8 - 2 6 36
1 - 2 -1 1
2 - 2 0 0
1 - 2 -1 1
1 - 2 -1 1
1 - 2 -1 1
1 - 2 -1 1
1 - 2 -1 1
2. Calculate the mean of those squares. Simply divide the sum of all these squared deviations ( which equals 42 in our case) by the number of scores (8 in our case), which gives us variance = 5.25.
Thus, a formula for variance is:
The formulas for variance and SD that we discussed here are applicable for a SAMPLE that you are testing. Now, if you want to generalise and calculate the results for the population, you would need to make one small change to your original formulas, that is: to divide not by N, but by N-1. This is what is called 'the degree of freedom'. Thus, your formulas for 'Estimated Variance' and 'Estimated SD' respectively are: