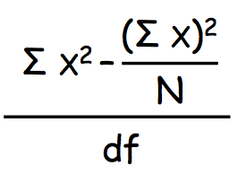
Also like with the t-test, there is ANOVA test for unrelated and related samples. In this post, I will only discuss the unrelated-subjects design: that is, when all the participants are tested only once.
ANOVA can also be two-ways, three-ways etc. - depending on how many independent variables there are in an experiment. Today I will look at the one-way ANOVA, which works with one IV. As always, I will cover the assumptions, logic behind the test and show step-by-step calculation using an example.
Assumptions
1. The groups should consist of independent samples of scores; that is, each participant should only contribute one score to the data.
2. The scores should be numerical: ratio or interval.
3. The data should be normally distributed
4. It is not necessary to have equal numbers of scores in each group.
With assumptions being so similar, why can't we perform a t-test to compare means of more than two groups?
Well, first of all, imagine we want to compare 6 different groups. To do so, we would need to conduct 15 different tests! That would get messy, and take lots of time.
But more importantly, every time we run a t-test the chance of get a Type I error increases - that is, to get a significant result by chance and accept experimental hypothesis by mistake.
Logic behind analysis of variances
In order to obtain a 'true' score we simply substitute the groups' means for each of the scores of corresponding groups. The groups' means are the best estimates of the 'true' scores, because we can assume that any deviations from the mean are due to error which is randomly distributed. Error scores, then, are easily found by subtracting 'true' scores from the corresponding observed scores.
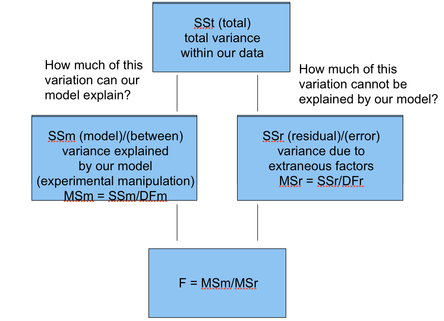
Now that we have three sets of scores - observed, error and true - we can calculate estimated variance for all of them (see post on Estimated Variance). Variance of observed scores shows how much variability there is in all of our data; we call it Total variance. Then, the Total variance is subdivided into True and Error variances. True variance reflects variability between the conditions, which is due to the experimental manipulation; we call it between groups variance. Error variance, however, shows how much variability there is due to other factors such as individual differences etc.; we call it within groups variance. Think of it as slicing a pie called TOTAL VARIANCE into two slices: error and true.
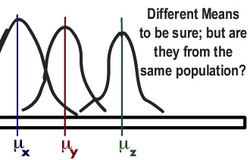
The null hypothesis states that difference between the groups (our true variance) is due to error. If this is true, difference between the true and error variances would not be very large (as, according to Ho, the variance of 'true' scores is due to error too). Therefore, if the difference IS significant, we can reject the null hypothesis.
To see whether this is the case, we need to make sure that our true variance is sufficiently larger than error variance; this is referred to as F ratio, and is calculated by dividing the true variance by the error one. Then, using the degrees of freedom, we find out whether the result is significant. If it is, it means that the difference between the error and true variances is significant enough to tell that the difference between the groups is NOT due to chance.
Degrees of Freedom
df for True scores (between-scores) = C - 1
df for Error scores (within-scores) = N - C,
where N = number of all the scores, C = number of columns (groups)
Calculation
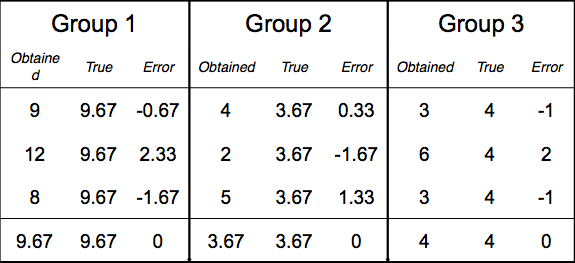
So lets see the example. Here is our data:
Ex^2 = 368.694
(Ex)^2 = 2704
(Ex)^2 / N = 300.444
df = C-1 = 3-1 = 2
variance estimate for true scores = 368.694 - 300.444 / 2 = 34.125
- Error scores:
Ex^2 = 19.334
(Ex)^2 = 0
(Ex)^2 / N = 0/9 = 0
df = N-C = 9-3 = 6
variance estimate for error scores = 19.334 - 0 / 6 = 3.222
Step 2: F-ratio
Step 3: Significance Table
In significance table, we simply look up the values of df for true (horizontally) and error scores (vertically) and find the critical value on their conjunction; for our case, 2 for true and 6 for error scores, F ratio should be equal or larger than 5.14. Our result is much larger than this, which means we can reject the Ho.
Computational formula
Step 1: Totals and Numbers
* Calculate the totals for obtained scores of groups:
T1 = 9+12+8 = 29
T2 = 4+2+5 = 11
T3 = 3+6+3 = 12
* Calculate the grand total G (sum up all the scores):
G = 9+12+8+4+2+5+3+6+3 = 52
* Calculate the number of scores: N = 9
* Find the df = N-1 = 9-1 = 8
Step 2: Total sum of squared scores:
Ex^2 = 81+144+64+16+4+25+9+36+9 = 388
Step 3: The 'correction factor' (this is simply a part of the formula for estimated variance expressed as G^2/N instead of (Ex)^2/N):
G^2/N = 52^2/9 = 2704/9 = 300.444
Step 4: Total sum of squares (also part of the estimated variance formula):
SS[total] = Ex^2 - G^2/N = 388 - 300.444 = 87.556
Step 5: Sum of squares between groups (true scores) and estimated variance. Here, we use the numbers from the step 1 and the correction factor from the step 3:
* SS[true] = T1^2/N1 + T2^2/N2 + T3^2/N3 - G^2/N = 29^2/3 + 11^2/3 + 12^2/3 - 300.444 = 280.333 + 40.333 + 48 - 300.444 = 68.222
* df = c-1 = 3-1 = 2
* Estimated variance[true] = SS[true]/df = 68.222/2 = 34.111
Step 6: Sum of squares within groups (error scores) and estimated variance:
* SS[total] - SS[between] = 87.566 - 68.222 = 19.344
* df = N-c = 9-3 = 6
* Estimated variance[error] = 19.344/6 = 3.222
Step 7: F-ratio
F = 34.111/3.222 = 10.6