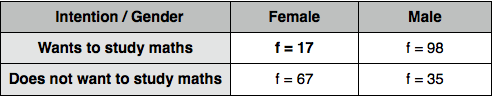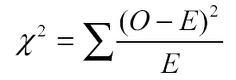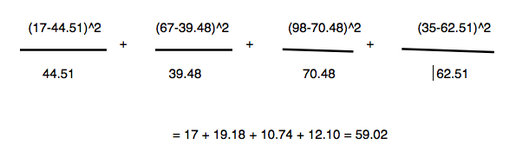- Are gay people more likely to be religious than straight people? (2 variables: religious belief and sexual orientation)
- Are male schoolchildren more likely to pursue academic career in maths than female ones? (variables: gender and programme of choice to study in university).
As always, I will explain the logic of the Chi-Square, show the calculation using an example and talk about Degrees of Freedom and Significance Testing.
Null Hypothesis
The statistical question is whether distribution of frequencies in the different samples so varied that it is unlikely that these all come from the same population.
We can see that there are much more boys than girls who want to study maths; these frequencies obtained in a research are called observed frequencies O. However, there is always a possibility that the data came from the same population and that the differences between the samples are only due to the chance fluctuations of sampling (Null Hypothesis). Therefore, we need to see how different each sample is from the population distribution defined by the Null Hypothesis. As ever, we don't have an access to the population data and have to estimate it from the sample characteristics.
Calculation
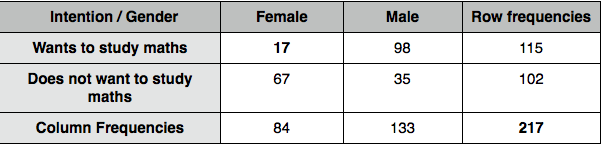
However, there were 17 out of 84 in the first sample and 98 out of 133 in the second sample who wanted to study maths; how do these figures correspond with our population expectations? We need to calculate the expected frequencies E for each of the cells, assuming that the null hypothesis is true (i.e. the nominal variables are unrelated) by using the formula: E = R*(C/N)
So, if Null Hypothesis is true, we would expect 115 out of every 217 female students to have an intention to study maths. Thus, the expected frequency for the first cell is:
84 * 115/217 = 44.51
Similarly, we would expect 102 out of every 217 to not have an intention to study maths:
84 * 102/217 = 39.48
Following the same procedure, we see that the expected frequency of males who want to study maths is 70.48 and those who don't - 62.51
Next step is to apply the Chi-Square formula:
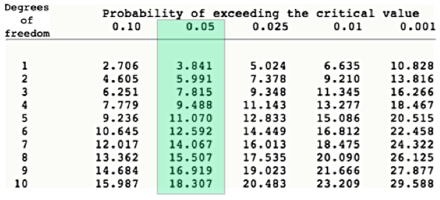
Degrees of Freedom
Significance Testing
Reporting the results
Potential troubles; partitioning
In this case, you can not go ahead with the Chi Square test and will have to use Fisher Exact Probability test instead (will be discussed in following posts)
2. Contingency tables with more than 2 categories: partitioning
Sometimes there are more than 2 categories (for example, if we want to compare alcohol consumption among the unemployed, part time and full time working individuals). In this case, expected frequencies, Chi Square and significance testing are carried out in exact same way. df will be bigger than 1 (with 2*3 tables, it will be 2 etc.), so be careful with those.
However, an association between the variables (here, alcohol consumption and employment status) won't tell us where exactly the difference lies. Thus, whenever our df is > 1, we will have to do partitioning: further Chi Squares which would separately test pairs of categories (say, employed full time vs. part time, full time vs. unemployed and part time vs. unemployed).
In this case, we will have to adjust the significance level accordingly. For the three separate Chi Squares our 5% significance level is divided by 3, which gives us a new significance level of 1.67% (0.01).