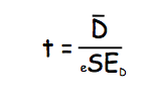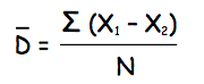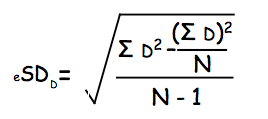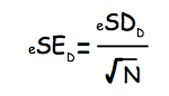
In this post, I will talk about within-subjects tests, their assumptions, calculation and significance testing. Before that though, I will quickly explain the difference between Parametric and Non-Parametric Statistics tests.
Parametric v Non-Parametric Tests
a) Parametric Tests are used when the data is normally distributed and when it is interval or ratio.
b) Non-Parametric Tests are used when the data is NOT normally distributed and when it is ordinal.
And this is it! So the only thing you need to do is to check the distribution and the measurement type of your data, and you will know which type of test to use. However, whatever type it is you choose to use, there is yet another decision to be made: whether to implement within-subjects or between-subjects design.
Within-Subjects v Between-Subjects tests
a) Within-subject design involves repeated measures of the same sample. In other words, the same participants are tested in different conditions/at different points in time. Example of an experiment could be, say, does memory decrease after frontal lobotomy? Clearly, we would have to test the same patients to find out: before and after the surgery. It is also used when there is no opportunity to have a control group due, for example, to a rare condition/illness.
b) Between-subjects design is all about measuring different groups of participants. So, for example, do bilingual children have a better memory? Obviously, the same child can not be bi-lingual and not bi-lingual at the same time, so we would need to test two different groups and then compare the results. In medical research, we would use this test to compare those who undertook a treatment and those who did not (control group).
Student's t-test for related samples
EXAMPLE
Within subject study on the effect of frontal lobotomy on memory: does memory decreases after the surgery?
Null hypothesis (Ho): there is no effect of frontal lobotomy on the memory. Ho predicts that the mean of the two samples (Before the lobotomy, After the lobotomy) will be identical, and they are drawn from the same population.
Alternative hypothesis (H1): there is an effect of lobotomy on memory. H1 predicts that the two samples (before and after the lobotomy) will have different means, thus these samples come from two different populations with different characteristics.
Independent Variable: lobotomy
Dependent Variable: scores on memory test
To answer the question of the research we need to compare the means of the two samples and find whether there is a significant difference between the two. To do so, we use the Student's t-test for related samples (parametric test because the data is numerical (scores on memory tests) and within-subjects design because we test the same participants). The calculation for the Student's t-test for related samples is as follows:
There you have it! Although it all seems like a notorious process, the math is actually quite simple and only features the formulas we've covered before: mean, Standard Deviation and Standard Error.
Degrees of Freedom and Significance Testing
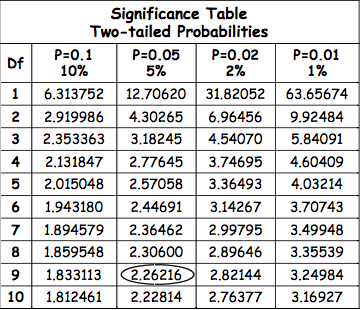
To test your results for the significance, you need to calculate the t-value and degrees of freedom, and then set the significance level (normally p<0.05). Basing on the p value and DF, use the significance table to find the critical value; then look at your t-value.
If +t > + critical value or -t < - critical value, we can accept the H1. It means that there is a statistically significant difference between the means of the two samples, and that this difference falls in the 5% of the extreme cases.
For example, imagine you have 10 participants. Degrees of Freedom in this case would be 10-1 = 9. Say, your t-value is 2.04, and you need to know whether this difference is significance at the 5% significance level. Look at the table below: