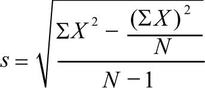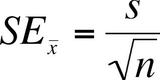
YES, it is possible - but only if this generalisation (or, inference) is done right. In this post I will talk about Inferential Statistics; it provides some essential rules which make it possible to draw conclusions about the population from the sample scores.
Rules of selecting a sample
Random sample means that everyone in a population of an interest should have an equal chance of being selected. This could be done, for example, by choosing every 5th or 4th person in a phone book, or knocking on every 10th door on every 20th street in a city.
As to the sample size, typically, the larger it is, the better. This is so because if the sample is large, then every possible score that occurs in a population has a larger chance of appearing in our data, thus making it a better representation of this population. I will talk more about the importance of having a large sample in the next section.
Standard Error
Imagine that we have 25 scores with a mean of 4.20. Out of this population we selected 20 samples of 4 scores each. Then, if we calculate the means for each of these samples, we would get 20 separate sample means, and each of them would be very different from our population mean of 4.20; we can get means of 6.00, 2.30 etc. The standard deviation for means of samples is what we call Standard Error. It could equal, for example, 0.89. This would simply mean that on average, the means of of our 20 samples differ from the population mean (which is 4.20) by 0.89. If we had fewer samples, for example, 10, the distribution of the means would be quite different, with a bigger deviation from the mean (bigger standard error) - in other words, the average of the sample means would differ more from the population mean if the number of samples was smaller. This is why the larger the sample the better it represents population.
Same is true for the scores from samples for experiments: their mean can be very different from the population mean - and standard error helps us to account for this. However, normally we only have one sample in the experiment - so how do we calculate the mean for means of numerous samples?
We can estimate the standard error from the sample characteristics. Firstly, there is a relatively easy way of using a SD of a sample to estimate a standard deviation of the population, which I discussed previously. The formula is what we call an Estimated Standard Deviation, and is exactly the same as a standard Deviation Formula, apart from the lower half of the formula is N-1 rather then N.