
I will discuss some of the assumptions, explain the logic behind the statistics and show a quick way of calculating the repeated measures ANOVA,
 In the previous post I discussed ANOVA for unrelated samples, which is an equivalent of a t-test for unrelated samples. Similarly, within-subjects ANOVA is an equivalent of a t-test for related samples. However, as I stated before, both ANOVAs can be used for comparing more than just two samples. I will discuss some of the assumptions, explain the logic behind the statistics and show a quick way of calculating the repeated measures ANOVA,
0 Comments
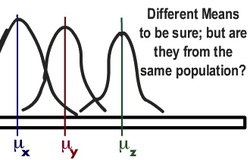 ANOVA is a statistics test which, exactly like a t-test, compares sample means to see whether the difference between these samples is statistically significant. However, unlike t-tests, ANOVA can be used to compare not only 2, but 3 or more samples - in fact, as many as you like! Also like with the t-test, there is ANOVA test for unrelated and related samples. In this post, I will only discuss the unrelated-subjects design: that is, when all the participants are tested only once. ANOVA can also be two-ways, three-ways etc. - depending on how many independent variables there are in an experiment. Today I will look at the one-way ANOVA, which works with one IV. As always, I will cover the assumptions, logic behind the test and show step-by-step calculation using an example.  Chi-square (X^2) is a statistical method used to analyse nominal (frequency) data rather than quantitative data obtained from continuous variables such as height, temperature etc. (scores) and requires between-subjects design. It is used when we want to compare frequency counts of different categories to see whether there is an association between the variables. For example: - Are gay people more likely to be religious than straight people? (2 variables: religious belief and sexual orientation) - Are male schoolchildren more likely to pursue academic career in maths than female ones? (variables: gender and programme of choice to study in university). As always, I will explain the logic of the Chi-Square, show the calculation using an example and talk about Degrees of Freedom and Significance Testing. Today we will be looking at the non-parametric test for unrelated samples: Mann-Whitney U Test.
As always, I will explain the calculation step by step using an example, and show how to test the result for statistical significance. First though, I will quickly recap the general assumptions for Non-Parametric tests and remind how to rank the data to make it suitable for Non-Parametric tests.  what do I do with this??.. Today I will look into the Non-Parametric tests. I will start with a quick recap on what Non-Parametric tests actually are and when it is appropriate to use them. I will also remind how to rank data to make it ordinal and how to deal with tied scores. This particular post will focus on the test for related samples (same participants tested in different conditions): its assumptions, calculation and significance testing.  I have covered parametric test for within-subject design. In this post, I will talk about the parametric test for between-subject design: Student's t-test for unrelated samples. Instead of looking at the differences between the pairs of scores (as t-test for related samples does), it looks at the differences between overall means of the two samples. I will cover the assumptions for this test, explain the calculation process and significance testing, and finally talk about the Levene's test, which is only implemented in t-test for unrelated samples.  In the previous post I mentioned that t-tests are used to compare two means in order to reveal whether they are significantly different. In order to transform the means into t-scores and perform the mean comparison, t-tests are conducted. There are two kinds of those: between-subjects and within-subjects, depending on the measure design of an experiment (I will elaborate on this and give you some examples further down). In this post, I will talk about within-subjects tests, their assumptions, calculation and significance testing. Before that though, I will quickly explain the difference between Parametric and Non-Parametric Statistics tests. 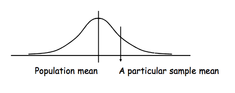 In this post, I will introduce you to t-scores and explain how they are similar to z-scores (remember those? They tell us how likely it is for a particular score to occur). I will also talk about t-distribution and its assumptions and explain the role which t-scores play in Hypothesis Testing; actual calculations and t-tests, however, will be discussed in the next posts.  I mentioned Inferential Statistics in earlier posts, but let's recap briefly: it is a set of rules which allow us to imply that results obtained from a sample are true for the population. Now, imagine that we got a correlation of 0.4 after testing the sample of 30 people. How do we know that such correlation occurs in the population as well? And, how do we know if the size of our sample was sufficiently big to be representative? In this post, I will explain what is meant by significance testing. In practice, it does not involve any calculation; in fact, there is a ready-made table of significance which simply tells you whether your result is significant enough or not depending on your sample size and correlation coefficient. However, I think it is important to understand the logic behind this table - and this is exactly what I will attempt to explain in this post. I will give the table in the end as well, so if you are not really interested in theoretical considerations at the moment you can safely go straight there. Correlation Coefficients: Pearson correlation, Determination coefficient and Spearman's rho10/21/2012 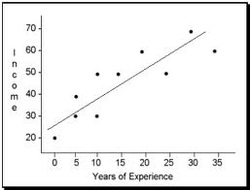 So far, I mostly talked about the ways to measure a single variable. However, most of statistical operations involve two or more variables; and what the experimenter is normally interested in, is the relationship between those variables. Today, I will talk about the ways to measure and illustrate it. The relationship between variables can be shown in two different ways: in a scattergram (like that on the right), or with the help of a single numerical index: correlation coefficient. The most common one is Pearson's product-moment correlation coefficient (or simply Pearson's correlation) which contains two pieces of information: 1) the closeness of the fit of the points of a scattergram to the best-fitting straight line through those points and 2) whether the slope of the scattergram positive or negative. It is important to understand that correlation coefficient does not replace the scattergram entirely, because it omits information about individual scores. However, it neatly summarises a great deal of information and is very useful when comparing several pairs of variables. |
AuthorI am a 21 years old Psychology undergraduate in Edinburgh University. The idea behind this site is to provide some help to fellow students, to make studying psychology (including stats...) as much fun as possible and motivate me not to skip those 9am lectures! Archive
February 2013
Categories
All
|
