z-scores v t-scores
* We transform scores into z-scores in order to get a z-distribution. It tells us how likely it is for a particular score to occur; Standard Deviation indicates how much a particular score differs from the scores mean.
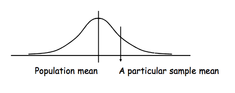
* Standard Error is a Standard Deviation of Sample Mean from a Population Mean. In other words, it is a measurement unit of how much the mean of our sample differs from a population mean.
We use z-scores to see the difference between a score and the mean using Standard Deviation as a measurement unit; we use t-scores to see the difference between the sample mean and population mean, using Standard Error as a measurement unit.
Therefore, t-score is a number of Standard Errors by which the observed sample mean differs from the population. T-distribution tells us how likely our sample mean is to be a population mean.
t-distribution
Application of t-scores: hypothesis testing
In psychology statistics, we use t-scores to compare two means of two different samples in order to test a hypothesis.
Hypothesis testing is an inferential statistics procedure which evaluate the credibility of a hypothesis for a population basing on the sample data. There are two hypotheses involved in any experiment: Null Hypothesis and Alternative (Experimental) Hypothesis.
Null Hypothesis states that there is no systematic difference between the means of two samples - that is, the samples come from the same population with the same characteristics.
Alternative Hypothesis states that there is a significant difference between the means of our two samples - and therefore, these samples come from two populations with differences in their characteristics.
If the difference between the means falls in the 95% of the cases, we accept the Null Hypothesis; it means that the difference is not significant enough for us to be sure it did not occur by chance. However, if the difference between the means fall in the 5% of the extreme cases, we may reject the Null Hypothesis and accept the Alternative Hypothesis instead. This would mean that there is a difference between the means, and the samples do indeed come from different populations.
t-scores allow us to determine whether the difference is sufficient enough to fall into those 5% of the extreme cases. I will show how to calculate a t-score in the next post.

